***
The teacher walks into the classroom and says ‘good morning’ to the children of a Year 5 class. He explains that today they will be doing something different…
‘I am going to set you some puzzles over the next session or two. Some of them, or all of them, may be unsolvable. I shall not tell you which are solvable and which are not. You are entitled to ‘give up’ at any time, however, I will only take you to have ‘given up’ when no one is left in the classroom who still wants to try. If there’s even just one person who still wants to try then you will not have ‘given up’. I should also explain that if you choose to ‘give up’ I will not tell you any answers. Is that clear?
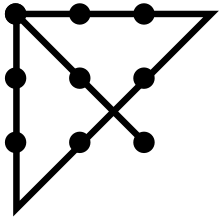
‘Now for the first puzzle. You will see, on the board, 9 dots that form a square:
DIAGRAM OF THE 9 DOTS AS ABOVE
‘The task is to cover all 9 dots with just four or less, straight, continuous lines. By ‘four or less’ I mean ‘not five or more’. By ‘straight’ I mean ‘not bent or curved in any way’. By ‘continuous’ I mean that, in principle, you ‘shouldn’t have to take your pen off the board to complete the task’. [It should be noted here that if they do take their pen off the board then that is not automatically a contravention of the rule. Only if they would have to in order to complete their ‘solution’. Also note that when explaining the rules do not demonstrate them. Once the rules have been explained, clarifications can only be made by the children ‘trying things out’.]
The teacher continues: ‘I shall not answer any questions. All I shall do is tell you when you break the rules. If you have a question then the only way to have it answered is to come up and try it. I shall tell you when you have broken the rules and I will tell you how you have broken the rules. Other than that I shall say nothing until later on when I may provide a clue or two. But remember if it is unsolvable then the clues won’t work. That’s for you to decide.
‘I encourage you to get up and try things out especially as you will not have any paper to ‘try out’ on. And remember: everything you each do will help the other members of the class in some way, so please: TRY THINGS OUT.
‘Now, who would like to come and start things off?’
***
This is the beginning of a lesson plan designed to enable primary school children to attempt the famous ‘9 dot problem’. I have been attempting to engage children of this age with this problem for the best part of 10 years but had usually found that I ended up having to show them how to do it, as they could get so far with the problem but then got stuck. I was convinced that the problem was in the way I was engaging them and not that it was too advanced.
Inspired by some features of the Socratic pedagogical method found in the Meno dialogue by Plato, I eventually devised this method. So far, it has yielded a 100% success rate with Years 4 – 8 (ages 8 – 13) children.
The main Socratic principles derived from Plato that inform this approach are as follows:
- The children can recover this knowledge for themselves if given the opportunity.
- The teacher only gives clues when absolutely necessary and draws the clues from the children’s own attempts wherever possible.
- There is the presence of uncertainty and the possibility of inconclusiveness (Greek: aporia). This is not, I will argue, stultifying but motivating.
One notable absent Socratic principle however is that of questioning. Even the use of effective questioning has been removed, or at least minimised, in this unusual session. The ‘teacher’ is as absent as possible whilst still retaining a guiding, pedagogical role. Here is a list of the salient pedagogical features of this lesson:
- Uncertainty as motivation
- Collective intelligence
- Collaborative learning
- Peer modelling
- Risk taking
- Time to ‘unfold’ the problem
- Creativity
- Overcoming fear
- Innovation
- Experimentation
- Logical, stepwise learning
Before I say something about each of these features let me start by continuing to outline the methods of the teacher during and at the end of the session.
The activity of trying to solve the puzzle is best done with an interactive whiteboard (on the squared paper setting). The reason for this is that it is the easiest way for the contributions to be preserved for all to see. Inevitably, questions will be asked. If this happens the teacher should resist answering them but remind them that they can only answer questions by trying them out. If they do and it clearly breaks a rule then the teacher should thank them and explain how what they have done has helped the class to better understand the rules. Remind them that every contribution is helpful. When a set number of contributions have been made (e.g. 5 or 10) the teacher then says that they will provide a clue. The clues - as often as possible - should be taken from the examples already on the board. For instance, it is quite common for someone to draw a line that extends beyond the limit of the implied square. This is sometimes done deliberately, and sometimes by mistake. If it is done, then however it is done, this makes a perfect clue. Alternatively, someone may draw something that resembles the ‘kite’ shape that the solution produces, so this too would make a good clue example. Once the clues have been provided it might be advisable to ask each subsequent contributor how they have used the clue. This gentle insistence brings their attention to the clue information. (Many of the children I have worked with have a habit of seeing the clues but then don’t use them.) Another good question to ask is: ‘What is unique about the clue example(s)?’ or ‘What do the clues have that the others don’t?’ From then on the teacher simply gives a new clue every time a child provides one. Other than that the teacher’s main tool is patience. One important principle to bear in mind when running this session is not ‘When can I jump in and explain something?’ but, instead, ‘How can I keep ‘out of it’ for as long as possible, intervening only when necessary?’ I describe this teaching principle as ‘absence’.
Uncertainty as motivation: Whenever I have run this session the children always respond with a slight measure of shock when faced with the possibility that they will not solve the problem and that they will not be told the answer. The children inhabit a culture of ‘back of the book’ answers and often tell me that they have never had an experience like this one. Very often some children will opt to ‘give up’ and some become quite aggressive in their insistence on this. However, I have never yet had a session where at least one member of the class did not want to continue. This provides an extremely important learning outcome, during and after the session, for all the children involved and I hope that the experience will stay with them for a long time.
A natural position in the ‘real world’ is one of uncertainty. When problems need to be solved in real situations it is often far from clear that there is an answer prior to one being found. Children need to have experienced this ‘real world’ possibility and be psychologically prepared for such an outcome much more than they currently are. Socrates, Plato and Aristotle all argued for aporia (‘puzzlement’, ‘perplexity, ‘inconclusiveness’) as a positive state, motivating one to seek for further knowledge or for a solution to the cause of the aporia. All too often children experience perplexity as a negative experience, a sign that they have failed or are not clever.
Collective intelligence, peer modelling and collaborative learning: All too often children are assessed on their individual achievements but many important individual insights and much individual progress is made in the context of interactive work. From this session you might think that the peer modelling would follow this pattern: where ‘the solver’ shows everyone else how it’s done. But it is quite the opposite. When the solver solves the puzzle the children are psychologically disposed to perceive the solver as ‘the hero’. Once the puzzle has been solved the first question to the solver should be: ‘Well done! Now, what gave you the idea to do this?’ In all cases so far, they have referred to an earlier example provided by another child. Interestingly, the child referred to is very often not a ‘gifted’ child. The teacher should continue this line of questioning to reveal a connected thread of ‘inspirations’. Once the ‘thread’ has been noticed by the class a shift occurs from seeing the solver as ‘the hero’ to seeing the achievement as a collective one.
Risk taking, experimentation, innovation and overcoming fear: Some of the gifted and talented pupils will often not want to get up and have a go until they feel that they know how to solve it. They will often sit and watch the others get up and try (but ‘fail’) and then step in at the end when they have seen the solution and swoop to make the victory strokes. An interesting observation from this behaviour is that they are afraid to try and fail at the task. Gifted students are therefore suppressing an experimental instinct and disallowing themselves to benefit from experimentation or develop the ‘art of learning from making mistakes’ in a social, collaborative context. At the end of the session I do not allow any pupils who refused to have a go to take any of the credit. This may seem a little harsh but I am sure you can see the value of this. The way I phrase it is to say: ‘Anyone in the classroom who got up and had a go can claim the credit for having solved what seemed to be an impossible task. Unfortunately, if you did not have a go, then, I’m afraid you can’t.’ After the session I show them examples from Leonardo da Vinci’s notebooks in which he can be seen to make all sorts of attempts that he simply crosses or scribbles out. This is one reason why he was such an innovator. The absence of paper to ‘try out’ on means that they have to ‘try out’ in front of each other which encourages experimentation.
Stepwise learning and the need for time to ‘unfold’ the problem: When I began doing this puzzle with classes of children I used to schedule it in at the beginning of a session, so would allocate no more that 25 minutes to the task. However, crucial to the success of this session is allowing the time for the children to slowly work it through. The process of ‘scaffolding’, that is to say, the inter-related way in which the children build and link their ideas, needs time. And this is just what they don’t usually have in a normal teaching context. I often receive the same criticism of the techniques that I teach: that there simply isn’t enough time, with all the demands of the curriculum, to use the approach I advocate. My response to this is that taking the ‘time-saving’ route of instruction and ‘explaining the answer’ is false economy. If a child does not have understanding of a topic or procedure then they will need to ask the teacher again and again for ‘the answer’ and the teacher will find that they need to reiterate the information many times. In the long run this is not the time-saving route it promised to be. Taking the time at the outset to allow understanding to be self-constructed in the child or children means that less reiteration is needed. The reason why teachers often feel the need to explain the answer themselves is because they are jumping ahead of the point that the children have reached. The solution to this problem is to question the children in such a way that they move step-by-step towards a deeper understanding. To carry this metaphor a little further, the teacher needs to observe which ‘step’ they are standing on in order to assess what is needed for them to be able to ascend to the ‘next step’. If the teacher is explaining the top step while the children are struggling with the first step then, naturally, the teacher will feel frustrated. This is when the teacher will feel that they need to simply provide the answer and the explanation.
The solution to the 9 dot puzzle:
This puzzle perfectly characterises the expression ‘think outside the box’ as the solution is lateral. There is a self-imposed limit perceived by the person trying to solve the puzzle that it must remain within the square implied by the dots. The solution can only be reached once they have noticed that there is no restriction on the length of the lines: